활성화 함수 (Activation Function)
딥러닝 모델에서 기본적으로 하나의 신경망은 ax + b의 함수 형태이다
즉, 입력값에 대한 출력값을 선형적으로 계산하게 된다.
이러한 ax + b 형태의 함수를 여러 층 쌓아도 여전히 선형 함수 형태이게 된다 (단층 신경망과 큰 차이가 없어지는 것!)
하지만 그렇다면 예를 들어 아래와 같은 모양의 이진 분류 데이터셋이 있다면, 이는 선형 함수로만은 분류가 불가능하다

위와 같은 데이터를 제대로 분류하기 위해서는
(일반적으로 일상의 데이터는 복잡해서, 위 데이터처럼 선형분류가 불가능하다)
입력값을 선형적으로 분류하는 것이 아닌 '꺾어줄 수 있도록'! 즉, 비선형적으로 분류해주도록 해야한다
이 때 사용되는 것이 활성화 함수인데, 선형 함수의 신경망을 비선형 함수로 만들어서 신경망의 복잡도를 높이는 역할을 한다

(a) 계단함수
계단함수는 특정 임계값에 따라서 0 또는 1을 내뱉는 활성화 함수를 의미한다.

하지만 계단함수는 값을 극단적으로 압축하여 (0 또는 1) 전달하기 때문에, 기존 데이터의 정보를 손실시키는 경향이 있다
또한 신경망을 훈련시키기 위해서는 함수의 형태가 미분 가능해야한다 (Gradient Descent를 이용한 학습법을 사용하기 위해서)
미분 가능하기 위해서는 함수가 매끈하게 생겨야하는데, 일반적인 계단함수는 매끈하지 않기 때문에 활성화 함수로 사용하기에는 어렵다
(b) 시그모이드(Sigmoid) 함수
시그모이드 함수는 계단함수를 곡선의 형태로 변경하여, 미분이 가능하도록 한 활성화 함수이다.
(종종 0~1 사이의 확률값을 추출하기 위한 이진 분류 문제의 output function으로 활용되기도 함)

시그모이드 함수는 작을수록 0에 가까운, 클수록 1에 가까운 연속적인 실수값을 내뱉으며,
일반적으로 우리가 알고있는 로지스틱(logistic) 함수라고도 한다
하지만 시그모이드 함수도 단점이 존재하는데
신경망이 깊게 쌓일 수록, 실수가 반복해서 곱해지므로 전달되는 기울기가 소실(Gradient Vanishing)될 수도 있다는 것이다
즉, 신경망이 깊어지면 가중치가 갱신되지 않으며 학습이 멈추게 된다
또한 함수의 값 중심이 0이 아니고, 항상 양수이기 때문에, 가중치에 대한 기울기가 항상 양수 혹은 음수가 된다
이는 기울기 업데이트가 지그재그 형태로 이루어지고, 학습 효율성을 감소시킨다
(c) 하이퍼볼릭 탄젠트(Hyperbolic Tangent, Tanh) 함수
Tanh 함수는 시그모이드 함수를 1과 -1의 임계값으로 scaling하여, 함수값의 중심을 0으로 맞춘 활성화 함수이다

시그모이드 함수의 zigzag 문제를 해소하기는 했지만
여전히 출력값이 실수이므로, 기울기 소실 문제의 가능성은 여전히 존재한다
(d) ReLU 함수
ReLU함수는 0과 입력값 중 큰 값을 내보내는, 즉 양수인 경우에만 값을 전달하는 활성화 함수이다.
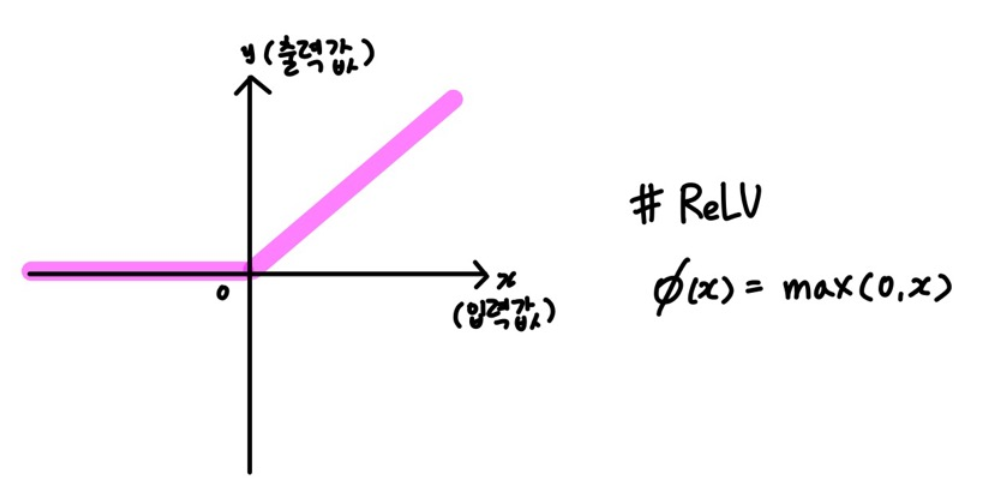
ReLU 함수는 0보다 큰 값이면 그대로 내보내기 때문에, Gradient Vanishing 문제가 어느정도 해소된다
또한 값을 비교한 후 바로 내보내기 때문에 연산이 매우 간단하고 빠르다는 이점이 있다
단, 모든 문제를 완벽하게 해결하는 것은 아닌데
그 이유는 큰 값의 양수가 반복해서 곱해질 때 여전히 Gradient Exploding의 가능성이 남아있고
특정 노드의 출력 값이 0이 나온다면, 그 이후의 레이어에서는 어떤 값이 나오든 학습이 이루어지지 않는 Knockout 문제가 발생한다
(e) LeakyReLU 함수
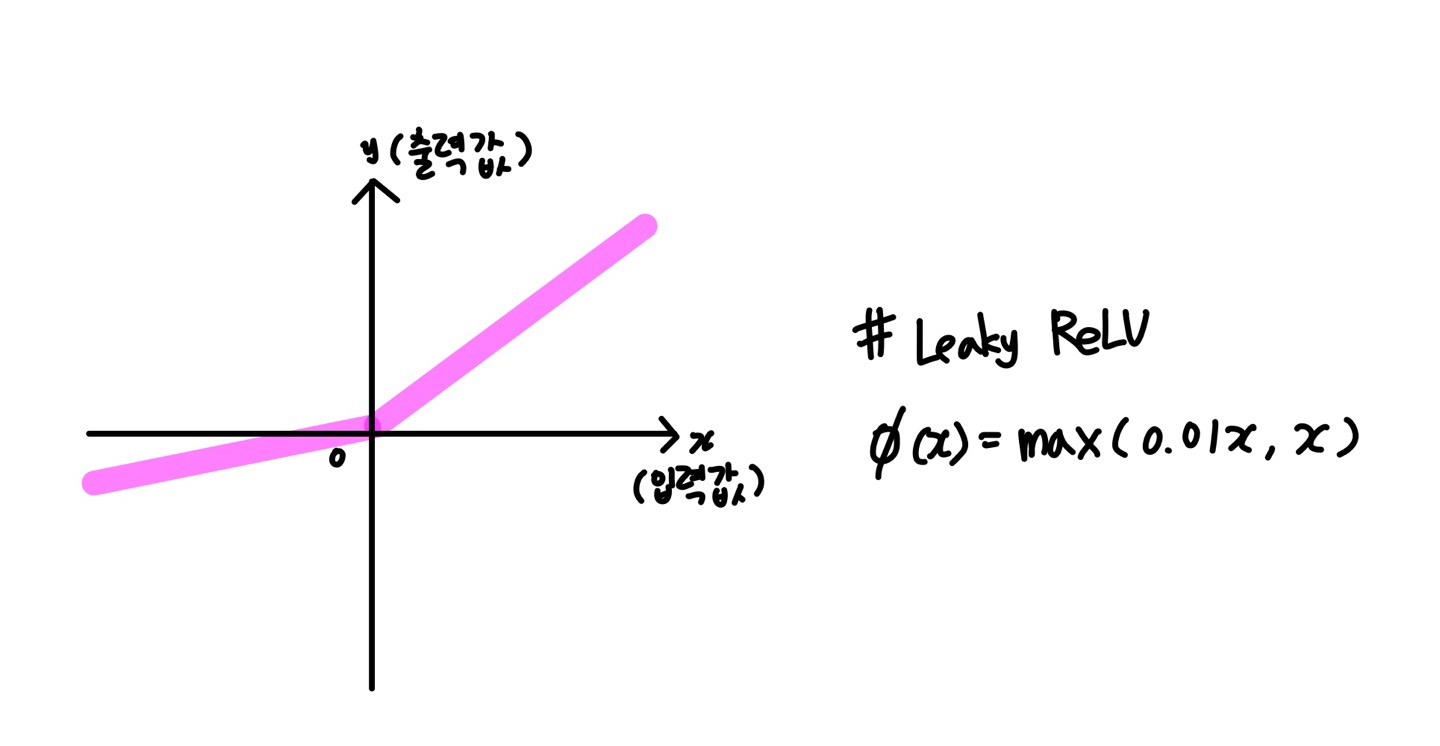
ReLU의 Knockout 문제를 해결하기 위한 활성화 함수가 LeakyReLU이다
0보다 작은 값에는 0.01을 곱함으로써 작은 값을 최대한 살리고자 한다.
그러나, 0.01을 곱하는 연산의 비용과 시간으로 인해, 사실상 ReLU를 더 많이 사용한다고 한다
또한 음수에 선형성이 생기게 되어서, 복잡한 분류에서는 사용이 적합하지 않다는 이야기도 있다
(f) ELU 함수
ELU는 max(0, x) 형태로 각져있는 ReLU를 exp를 사용하여 부드럽게 만든 것이다

ELU는 ReLU와 다르게 0에서도 부드러운 연결을 보여주며, 음의 출력을 생성할수도 있다.
또한 음수에서도 비선형성을 보여주기 때문에 비교적 복잡한 환경에서도 사용할 수 있다
하지만 ReLU에 비해서 성능이 크게 증가하지는 않고,
exp 함수의 사용으로 인해 이 또한 연산량이 늘어나게 된다
각 활성화 함수의 영향 확인하기

앞서 위에서 언급한 데이터셋을 실제로 활성화 함수를 바꿔가며 학습했을 때, 경계가 어떻게 변화하는지 볼 수 있다 (참고 링크 중 첫 번째, 플레이그라운드 참고)
Linear, 즉 활성화 함수를 적용하지 않았을 때는 아무리 학습해도 제대로 공간을 나누지 못하는 것을 알 수 있다
Sigmoid를 적용했을 때는 비교적 느리게 학습하고, 공간의 경계가 부드러운 곡선 형태인 것을 알 수 있다 (출력값이 0과 1 사이의 실수값으로 변환되기 때문으로 추정)
ReLU를 적용했을 때는 매우 빠르게 학습하고, 공간의 경계가 각져있는 것을 알 수 있다 (출력값이 그대로 임계값으로 사용되기 때문으로 추정)
참고
Tensorflow — Neural Network Playground
Tinker with a real neural network right here in your browser.
playground.tensorflow.org
- 라쟈링가파 샨무갸마니, 『컴퓨터 비전과 딥러닝』, 에이콘출판(2018)
- https://gooopy.tistory.com/56
- https://balmostory.tistory.com/52
- https://syj9700.tistory.com/37



